- パチセブントップ
- コミュニティ
- パチ7自由帳トップ|ブログコミュニティ
- コラム(ブログ)詳細
【解説】1/11より先に1/170が引きたい!
【解説】1/11より先に1/170が引きたい!
-
sin sparkさん
面白いものを作る人になりたい。 ちょっとプログラミングができるアクロスおじさんです。 - 投稿日:2023/01/05 22:53
軽く残業を終えた午後7時30分。
駅ナカで夜飯を食べようと待っていると、Twitterでこんな投稿を目にしました。
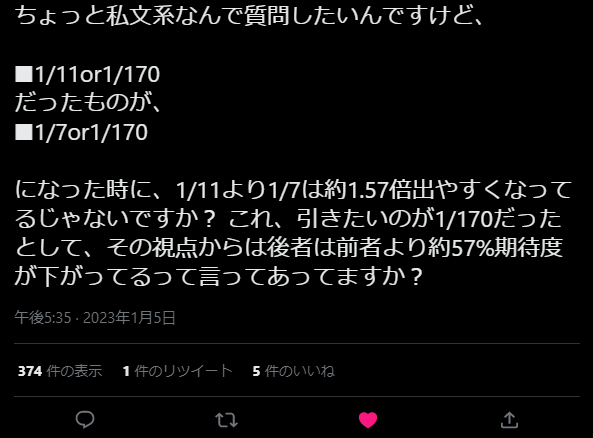
あれ?A:Bじゃないかな?と考えるも、このとき確証がいまいち持てなかった私。
なぜか非常にまじめに考えてしまったので、ここに記録を残しておきます。
【本日の結論】
引きたくない確率をA、引きたい確率をBとすると、Bを先に引ける確率pは
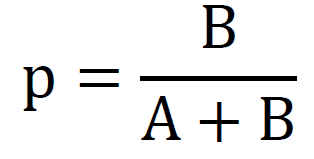
はい、予感どおりの結果でしたね。Twitter投稿にちゃんと回答すると
A = 1/11のとき、p1 = 約6.08%
A = 1/7のとき、p2 = 約3.95%
1/7のときの期待度は、1/11のときと比べ約65.0%となります。(=p2/p1)
…って、よく考えたらAタイプのBR比とか当たり前にこの式で計算してるんですよね。
例えばA = 1/256 (RB)、B = 1/240 (BB)とすればBBを引ける確率は上記pで計算できます。
で、確証を持てなかった私はこのpで求まることを「証明」していました。
その中身を以下に書きます。
※ここから先、数式がたくさん出てきます。苦手な方はご注意ください。
とはいえ、実は高校数学レベルですべて解決できます。
【p = B / (A+B) の証明】
お話を始める前に、ある確率:Cを定義しておきます。
このCは「AでもBでもない確率 = 継続」として次式で定義します。
C = 1-A-B
では、Aを引くと終わるCZにおいて、当たりBを引ける確率を考えていきましょう。
1回転目にBを引ける確率s1は当然ながら
s1 = B
ですね。一方で1回転でCZが終わらない確率は先ほど定義したCで表されます。
次に2回転目を考えます。2回転目に当たりBを引ける確率は
s2 = C×B
となります。Cが乗算されているのは1回転目でCZが終了しないことが条件だからです。
一方で、2回転回してもCZが終わらない確率はC×Cとなります。
3回転目。ここで当たりBを引ける確率は、
s3 = C×C×B
となります。s2に比べCが1回多くかかっていますね。
こんなことを考えながら無限にハマる可能性を考えると、t回転目に当たりBを引ける確率は

となります。
ここからが本番。ここまで述べてきたs1、s2、s3、・・・はすべて当たりBを引けた事象です。
ということで当たりBを引ける確率pはクソハマりした場合、つまり無限回ハマりまで考えると
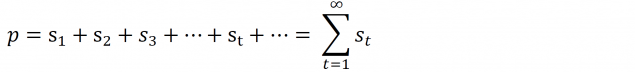
となります。Σが出てきました。高校数学が分からなくなってくる嫌な奴でしたね…。
さてそんな高校数学において、s1~…~stの形も見たことがありませんか?
実はこれ「等比数列」といいます。そしてこれを無限に足し算する「無限等比級数」という
言葉も、理系の方なら埃をかぶった頭の隅のさらに端っこに眠っているかもしれません。
で、そんな「無限等比級数」の解を求める方法はこんな方法でした。
①t=1~t=nまでの和(pn)を求める。実はこんなテクニックなことができる。(C≠0が条件)
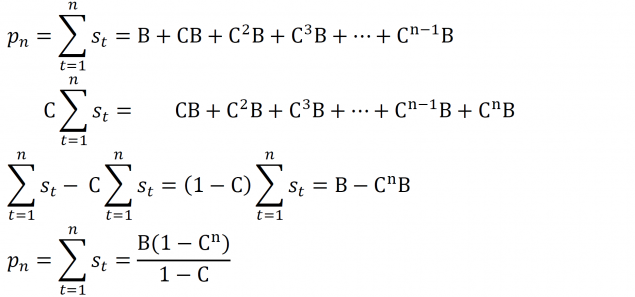
②pnをp→∞に発散させてpを求める。ここで0<C<1を使うとpを簡単な形で表せる。
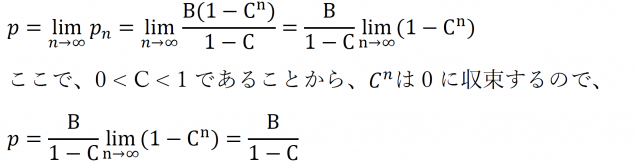
③Cの定義 (C = 1-A-B)を思い出してpを少しだけ変形する。
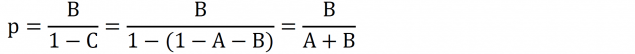
結果、冒頭の「結論」で述べたBを先に引ける確率pと一致する。[Q.E.D]
以上です。ね?簡単でしょ?((
【追伸】
証明を思いついてウキウキしながら帰ったら、自転車に乗りながらBR比の話を
思い出し、「あれ?すごく簡単な話じゃん…(´・ω・`)」となったのがハイライトでした。
本当にありがとうございました←
4
sin sparkさんの
共有する
コメントを送る
パチ7自由帳月間賞│特集記事
パチ7自由帳ランキング
-

-
4 8
-

-
3 0
-

-
3 0
-

-
3 2
-

-
3 0
-

-
3 2
-

-
2 0
-

-
2 0
-

-
2 2
-

-
1 2






このコラムへのコメント(4 件)
豪腕が一番の正解ですね!!((ぉ
技名らしい単語…たとえば他にも「部分分数分解」とか
「カージオイド」なんていかがでしょう?←
実質素早くBを引くゲームになるので、
それで間違いありませんbb←
数式はサッパですが、要は引きたいやつを引ける豪腕なら負けないってことですね!←違う
それはそうと、「無限等比級数」聖闘士星矢で出て来そうwwwジェミニ辺りでwwww
考えないことにした
要は引きゃあ良いんだよ、引きゃあw